Как сделать шар из бумаги схема: Как сделать шар из бумаги — схема своими руками 6 способов
Шар из бумаги своими руками: шаблоны и схема
Близится Новый год, а это значит, что пора задуматься о стильных праздничных украшениях. Можно, конечно, сходить в магазин и выбрать те шарики и игрушки, которые есть в наличии. Но к следующему празднику обязательно захочется чего-нибудь новенького. И что же, снова идти за покупками? Так не хватит ни денег, ни свободного места даже в самой просторной квартире. Но выход есть – яркие элементы декора можно без труда смастерить самостоятельно. Так квартира будет выглядеть каждый раз по-новому, а шкафы не придется загромождать ненужными коробками. Как ни странно, самые яркие и эффектные украшения получаются из самых простых материалов: бумаги, картона и даже пластиковых бутылок. Для их изготовления не потребуется никаких художественных способностей, достаточно просто следовать инструкциям. В этой статье мы расскажем, как смастерить шар из бумаги быстро и легко своими руками.
Создаем красивой и объемный шар из бумаги своими руками
Какие материалы можно использовать для изготовления шара:
1)Обыкновенные салфетки. Основным их плюсом, безусловно, является доступность. Для мелких шаров берите салфетки меньшего формата, а для больших – формата 30 на 30 сантиметров. Салфетка может быть любого цвета, но на ней не должно быть никаких рисунков в виде цветочков или Микки-Маусов – наш шар это не украсит.
Основным их плюсом, безусловно, является доступность. Для мелких шаров берите салфетки меньшего формата, а для больших – формата 30 на 30 сантиметров. Салфетка может быть любого цвета, но на ней не должно быть никаких рисунков в виде цветочков или Микки-Маусов – наш шар это не украсит.
2)Гофрированная бумага. Шары из этого материала смотрятся очень интересно, материал достаточно пластичен и позволяет легко создавать объемные фигуры. Также большим плюсом является то, что из гофрированной бумаги можно сделать шары большего диаметра, чем из салфеток (все зависит только от ширины рулона).
3)Бумага тишью. Это слово может многим показаться незнакомым, но такую бумагу вы наверняка уже видели. Ее обычно используют для упаковки каких-либо предметов – например, кладут внутрь обувных коробок. А вот из бумаги тишью ярких цветов поучаются очень нежные и эффектные поделки. Основным ее плюсом является полупрозрачность, поэтому она красиво смотрится в подсвеченном виде. Кстати, такой материал еще называют папиросной бумагой.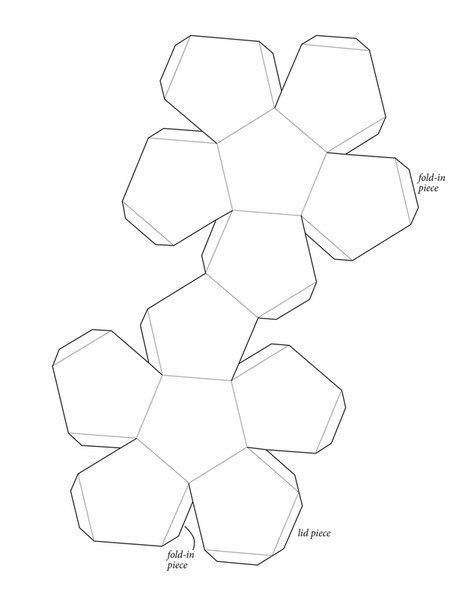
4)Последним пунктом выделим небумажные материалы для изготовления декоративных шаров. К ним относятся ткани, которые хорошо держат форму в сложенном состоянии – например, органза и фатин. Белые шарики из ткани будут очень мило выглядеть на зимнем торжестве, так как они похожи на пухлые снежинки или снежки. А если сделать шарики из оранжевой ткани, то получатся мандарины! Как видите, фантазии нет предела.
Итак, мы рассмотрели различные типы бумаги (и даже ткани) из которых можно смастерить объемные шары. Далее, в мастер-классе мы расскажем, как сделать шар на основе салфеток. Шары из иных материалов делаются точно по такому же принципу.
Для изготовления объемного шара из салфеток потребуется:
- шестнадцать бумажных салфеток (если салфетки двухслойные, то можно взять восемь)
- ножницы
- проволока
- степлер
- ленточка (на нее мы подвесим шар)
1)Нам потребуется шестнадцать бумажных салфеток – по восемь для каждой стороны шара. Если у вас двухслойные салфетки, аккуратно разделите их на листы.
Если у вас двухслойные салфетки, аккуратно разделите их на листы.
2)Берем одну салфетку и складываем ее «веером», посередине скрепляем степлером.
3)То же самое по шаблону повторяем еще с семью салфетками.
4)Кладем все заготовки «стопочкой» друг на друга и соединяем салфетки между собой.
5)Аккуратно ножницами закругляем края салфеток. Следите, чтобы при этом они лежали ровно.
6)Расправляем салфетки в разных плоскостях. У нас должна получиться половинка шара.
7)По этой же схеме делаем вторую заготовку.
8)Теперь необходимо соединить две половины шара между собой с помощью кусочка проволоки. Оставьте небольшую ее часть свободной и загните крючком.
9)Из ленточки делаем петельку, чтобы подвесить шар к потолку или на новогоднее дерево. Внутрь шара лента будет крепиться на крючок из проволоки, который мы сделали в предыдущем шаге.
10)Поделка готова!
Разбираем идеи по использованию объемных бумажных шаров
Самый простой вариант – это шары одного или двух цветов, которые подвешиваются к потолку на лентах разной длины. К сожалению, не каждое потолочное покрытие подойдет для такого декора – для этого на нем должны быть деревянные или пластиковые рейки, на которые можно будет закрепить ленты. Чаще всего такой способ используется для украшения офисных помещений.
К сожалению, не каждое потолочное покрытие подойдет для такого декора – для этого на нем должны быть деревянные или пластиковые рейки, на которые можно будет закрепить ленты. Чаще всего такой способ используется для украшения офисных помещений.
Одиночные шары можно превратить в фантастические цветы и украсить ими праздничный стол. Из более крупных заготовок получаются пионы, а мелкие похожи, скорее, на кустовую гвоздику.
Объемные шары очень стильно смотрятся на различных коробочках и пакетах с подарками. Перевозить такие поделки следует осторожно, чтобы украшение не помялось.
Видео по теме статьи
Более подробно посмотреть, как смастерить шар из бумаги разных типов, можно в следующих видео. С пошаговой инструкцией от опытных декораторов легко разобраться с непонятными элементами и без труда справиться с изготовлением этих стильных украшений.
youtube.com/embed/uHWuChq6HFI?start=87&feature=oembed» frameborder=»0″ allow=»accelerometer; autoplay; encrypted-media; gyroscope; picture-in-picture» allowfullscreen=»»>Как сделать цветочный шар из бумаги. «Цветочные шары»
Светлана Большакова
Здравствуйте, дорогие друзья! Недавно я получила задание : сделать шары из искусственных цветов для украшения коридора в детском саду. Опыта у меня в этом деле не было (то есть я делала шар из салфеточных роз, которые приклеивала термопистолетом. Пост «Поделки из гофротрубочек» . Фотоотчёт о МК с сотрудниками детского сада). Но за дело взялась, конечно. Вот один из шаров :
Но за дело взялась, конечно. Вот один из шаров :
Я купила пенопластовые шарики D = 6 см,
Покрасила их зелёной акриловой краской, ввернула шуруп
Купила букеты искусственных цветов , сначала по три на каждый шарик, потом докупала. В итоге на каждый шарик пошло по 8 букетов, в каждом букете по 5 веточек.
Веточки «откусила» плоскогубцами, примерно по 10 см
К шурупу туго привязала ленточку и стала вставлять веточки в шарик, иногда пользовалась шилом, иногда так вставляла
Вот что у меня получилось :
Вот мы их повесили к потолку, ввернув в плитку шурупы с полукольцом
А обрезкам от букетиков мои девчонки сразу нашли применение
Налепили цветов из пластилина
Девочки, может кто-то из вас более профессионально занимался таким делом и может дать дельный совет. Я буду очень благодарна!
1. РОМАНТИЧЕСКИЙ ПОДАРОК НЕВЕСТЕ ИЛИ ВОЗЛЮБЛЕННОЙ. ПОДЕЛКА В ФОРМЕ ШАРА ИЗ ЖИВЫХ ИЛИ ИСКУССТВЕННЫХ ЦВЕТОЧКОВ
Если вы хотите подарить
оригинальный подарок своей маме на День рождения или сделать необычный
аксессуар для невесты к свадьбе , то эта статья для вас! Здесь вы найдете полезные идеи, схемы с инструкциями,
мастер-классы, видео уроки , с помощью которых можно сделать своими руками красивый шарик из цветов.
Самый популярный материал для изготовления шаров
из искусственных цветов это бумага . Умельцы делают потрясающие шарообразные поделки с цветочками
из гофрированной и цветной бумаги ,из газет и картона. Но кроме бумаги для изготовления таких поделок можно успешно использовать кусочки кожи,
атласные или рапсовые ленты , отрезки полотна из хлопчатобумажных или шерстяных ниток.
Существует огромное количество способов складывания шаров из самодельных цветов. Например, очень красивые композиции складывают из бумаги в технике кусудама (направление в искусстве оригами). В одном из предыдущих материалов мы рассказывали вам, как делать своими руками уникальные объемные поделки в технике модульного оригами . Шары счастья (или кусудамы) оригамисты делают похожим способом. Но вместо модулей треугольной формы для складывания композиции в форме шара используются бумажные цветы с лепестками разной формы.
Шарами из искусственных цветов можно красиво декорировать зал для детского праздника, банкетный стол, помещения для юбилеев и свадеб.
Вы можете сделать своими руками изящные
аксессуары для свадебного мероприятия — шары из белых цветов (как искусственных, так и натуральных),которые заменят
свадебные букеты для подружек невесты. А разноцветные шарики из небольших бумажных цветочков будут интересно смотреться на вазах и в композиции свадебного дерева,
в букетах из конфет .
Из шарообразных поделок с большими и маленькими цветками дизайнеры делают интересные композиции в виде декоративных деревьев — топиарии. Говорят, что топиарии, украшающие подоконники, могут притягивать удачу в дом! 🙂
Как можно сделать своими руками шары из живых цветов? В качестве основы можно взять круглую флористическую губку. Берем цветочек (отличный вариант — гвоздика), отрезаем стебель, оставляя 4-5 см. Втыкаем заготовки в губку, красиво оформляя цветочный шар.
2. ПРОСТОЙ В ИСПОЛНЕНИИ ШАРИК ИЗ БУМАЖНЫХ ЦВЕТОВ. ИНСТРУКЦИЯ ДЛЯ НАЧИНАЮЩИХ
ИНСТРУКЦИЯ ДЛЯ НАЧИНАЮЩИХ
для изготовления заготовки для шара возьмите 3-4 листа тонкой (можно гофрированной бумаги) и одновременно сложите их гармошкой;
Кусочком ленты стягиваем заготовку по середине, срезая края и придавая желаемую форму с обеих сторон заготовки;
Каждую складочку приподнимаем по отдельности. получаются лепестки будущего цветка;
Аккуратно расправляем каждый лепесток, удерживая середину заготовки;
Для оформления разноцветного бумажного шарика используйте цветную бумагу.
3. МАСТЕР-КЛАССЫ И СХЕМЫ. ДЕЛАЕМ СВОИМИ РУКАМИ ОРИГИНАЛЬНЫЕ КУСУДАМЫ И ШАРИКИ ИЗ БУМАЖНЫХ ЦВЕТОВ
Вариант №1:
МАСТЕР-КЛАСС. КАК СДЕЛАТЬ ОЧЕНЬ КРАСИВУЮ ПОДЕЛКУ ИЗ БУМАЖНЫХ ЦВЕТОВ В ФОРМЕ ШАРА. УЧИМСЯ ПРАВИЛЬНО СКЛАДЫВАТЬ ЛЕПЕСТКИ,СОБИРАТЬ ЦВЕТОЧКИ И ФОРМИРОВАТЬ ШАР — ЗАМЕЧАТЕЛЬНОЕ УКРАШЕНИЕ НА ЕЛКУ К НОВОМУ ГОДУ ИЛИ НА ОКОННУЮ ШТАНГУ К ДЕТСКОМУ ПРАЗДНИКУ .
Вариант №2:
КАК СДЕЛАТЬ ЦВЕТОЧКИ
ИЗ БУМАГИ И СЛОЖИТЬ ИЗ НИХ БОЛЬШОЙ ШАР В ТЕХНИКЕ ОРИГАМИ КУСУДАМА. ПОШАГОВАЯ ИНСТРУКЦИЯ С ФОТО .
ПОШАГОВАЯ ИНСТРУКЦИЯ С ФОТО .
Вариант №3:
УЧИМСЯ ДЕЛАТЬ КЛАССИЧЕСКУЮ МОДЕЛЬ КУСУДАМЫ СВОИМИ РУКАМИ. ПОШАГОВАЯ СХЕМА И ФОТО ИЗГОТОВЛЕННОГО ПО СХЕМЕ ЦВЕТОЧНОГО ШАРА .
Вариант №4:
СХЕМА ОРИГИНАЛЬНОГО ШАРА В ТЕХНИКЕ КУСУДАМА С ЦВЕТОЧКАМИ В ВИДЕ ЗВЁЗДОЧЕК. ЗАМЕЧАТЕЛЬНЫЙ ВАРИАНТ ДЛЯ ИЗГОТОВЛЕНИЯ САМОДЕЛЬНЫХ ЁЛОЧНЫХ ИГРУШЕК НА НОВЫЙ ГОД .
Вариант №5:
КАК СДЕЛАТЬ ЦВЕТОЧНЫЕ .
Вариант №6:
ОЧЕНЬ КРАСИВЫЙ ШАРИК, КОТОРЫЙ ВЫ СМОЖЕТЕ СОБРАТЬ ИЗ ВЫРЕЗАННЫХ БУМАЖНЫХ ЗАГОТОВОК ПО ШАБЛОНУ. ЖЕЛАТЕЛЬНО ИСПОЛЬЗОВАТЬ ЯРКУЮ ЦВЕТНУЮ БУМАГУ ДЛЯ РАБОТЫ .
Вариант №7:
КАК СДЕЛАТЬ СВОИМИ РУКАМИ
Уже совсем скоро начнется предновогодняя суета и для большинства родителей встанет вопрос украшения класса или группы в детском садике. Предлагаем вам оригинальную новогоднюю поделку в школу или садик, которую можно сделать вместе с ребенком. Поделка бумажный шар из цветов станет замечательным украшением класса или подарком, который ребенок сделает своими руками. На первый взгляд кажется, что поделка сложная. Однако сделать ее очень просто.
На первый взгляд кажется, что поделка сложная. Однако сделать ее очень просто.
Для работы понадобится:
Лучше взять клей-карандаш, он склеивает быстрее и прочнее. Нарежьте цветную бумагу квадратами со стороной 7 см. Наш шар будет состоять из 12 цветков, каждый цветок из 5 лепестков. Всего необходимо 60 квадратиков. Мы сделали 2 вида цветков. Цветовые сочетания можно подобрать различные, а можно сделать однотонные цветы, например из белой бумаги, тогда наш шар будет похож на пушистую снежинку.
Поделка бумажный шар из цветов
Сложите квадрат по диагонали
Согнете уголки получившегося треугольника к центру. Получился ромб, но гораздо меньшего размера.
Отогните верхние слои ромба так, как показано на фотографии. Должен получиться вот такой трилистник.
Загнем уголки трилистника. Хорошо проглаживайте пальцами линии сгиба.
Теперь сложим крайние лепестки трилистника пополам вдоль
Свернем заготовку, прижав края друг к другу.
Склеим края заготовки. Прижмите их плотнее друг к другу, чтобы хорошенько склеить. Получился лепесток одного цветка.
Сделаем несколько таких лепестков и склеим их между собой.
Для одного цветка мы взяли 5 лепестков
Оттенки лепестков в одном цветке можно комбинировать
Начинаем склеивать цветки лепестками между собой.
В итоге получается вот такой яркий шар. Через центр шара пропускаем цветной шнур, предварительно смазав его клеем. Конец шнура можно украсить кисточкой. Для украшения класса или группы сделайте несколько таких бумажных шаров из цветов.
Любите ли вы цветы? Нелепый вопрос. Если человечество ещё не созрело для того, чтобы усадить всю планету цветами в знак всеобщей любви и признания, можно сделать это своими руками – шары из цветов. Да, букет, составленный флористами, привычен и никогда не утратит актуальности, но задумывались ли вы когда-нибудь, почему форма круга, а в объёме — шара так привлекает? Это солнце, это источник жизни и капля влаги в невесомости, это символ гармонии и совершенства бытия.
Это можно сделать самому
Не верите, что сотворить такую красоту способны своими руками? Попробуйте, непременно получится и доставит удовольствие не только результат, но и сам процесс. Как говорят французы, кто умеет творить, тот умеет жить. Всё доступно, легко выполняется. Попробовав одну, самую простую модель, фантазия подскажет массу вариантов, несложных для исполнения.
Из чего творится чудо?
Помните Цветаевское «Когда б вы знали, из какого сора растут цветы, не ведая стыда…»? Из самых разных материалов можно сделать шар из цветов своими руками. Во-первых, вырастить великолепное украшение стен загородного дома, балконов и лоджий — живые цветы именно шарообразной формы. Для украшения праздника, подарка – сделать из ткани, лент, бумаги, салфеток, готовых искусственных цветов. И понадобится-то для этого лишь основной материал, пенопластовая основа, ножницы, клей, некоторые мелочи, и желание.
Шары из живых цветов
Для особого случая создают трогательный шарик из живых цветов. Чаще всего для этого используют доступные в любое время года розочки и гвоздики. Они устойчивы, имеют прочный стебель, хорошо держат бутон. Технология проста. Для основы понадобится специальная флористическая губка, не обязательно шарообразная. В цветочном магазине можно приобрести и брусочек, из которого легко с помощью ножа сотворить шар не такой уж и строгой формы. Затем нужно поместить его в воду, чтобы хорошо пропитался. В это время стебли цветков обрезаем, оставляя до 5 см. Сколько понадобится бутонов? Это всегда зависит от диаметра шара. Давайте исходить из того, что для 8-сантиметровой в диаметре основы понадобится 20 — 40 цветков. Подставка для торта подойдёт, чтобы работать дальше. В клей ПВА, смешанный в равных количествах с водой, опускаем стебельки и начинаем сверху вставлять бутоны, равномерно покрывая основу. Заполнили все, кроме нижней части? Теперь осторожно перенесите шар на декоративный горшочек. Можно обойтись даже без клеевого скрепления. Украшение готово. Поверьте, вариантов работы много, и они сами приходят на ум, стоит только начать.
Можно обойтись даже без клеевого скрепления. Украшение готово. Поверьте, вариантов работы много, и они сами приходят на ум, стоит только начать.
Великолепие из бумаги
Бумажные цветы могут выглядеть совсем живыми, быть декоративными и нарядными даже в обыденной обстановке. Работа с бумагой доставляет много радости. Это привычный и пластичный материал. Начните с простейших изделий. Для основы найдите или сделайте сами пенопластовый шар любого подходящего размера. Предлагаем изготовить цветы из обычной цветной бумаги с помощью дырокола (продаются в виде 6-листиковых цветков, хорош 2,5 см.). Нужны ещё булавки с бусинками, шпилька для волос, если шар будет подвешиваться. Дыроколом набиваем около 70 цветков.
Соединяем, накладывая друг на друга, по 2 цветка, немного глубже прорезаем линии между лепестками. Чуть-чуть пальцами присбориваем края для придания объёма, булавку с нанизанным цветком втыкаем в основу, для большей прочности, закрепляя клеем (очень удобен так называемый клеевой пистолет). Вы сами определите, как близко нужно расположить цветки, каких цветов выбрать бумагу, как и куда поместить готовое украшение. Шар из цветов своими руками из бумаги делать очень приятно. Верьте — всё получится! Желающий сотворить цветы плохого сделать не может!
Вы сами определите, как близко нужно расположить цветки, каких цветов выбрать бумагу, как и куда поместить готовое украшение. Шар из цветов своими руками из бумаги делать очень приятно. Верьте — всё получится! Желающий сотворить цветы плохого сделать не может!
Самые нарядные
Правду говорят, что цветок, как любовь – ему нужно время, чтобы расцвести. Самые разные цветы можно изготовить из крепированной бумаги. Она хорошо поддается форматированию, создает объемные формы и выглядит живой в любом изделии. Из неё можно изготовить и розы, и гвоздики, и игольчатые астры, васильки, и все, что захотите.
Основой может быть не только прочный пенопласт, но и шар из ниток. Берёте шерстяные, синтетические или любые из имеющихся под рукой, пропускаете их через тюбик с клеем (лучше — ПВА), надуваете круглый резиновый шарик и постепенно наматываете нити, создавая достаточно плотную основу. Когда клей затвердеет, осторожно пальчиками отслоите в нескольких местах шарик от нитяного корпуса, проколите его и извлеките. Далее с основой можно работать по-разному: приклеить ленту, оставить без покрытия.
Далее с основой можно работать по-разному: приклеить ленту, оставить без покрытия.
Берём гофрированную бумагу, нарезаем лентами шириной 3 — 7 см., длиной 50 — 60 см. Один край немного растягиваем, далее, в зависимости от формы будущего цветка, либо нарезаем край, либо, если будет роза, не трогаем ножницами. Формируем цветок так: первые 3 — 4 см. скатываем в плотный рулончик, затем свертывание ослабляем, край цветка отгибая наружу. Получится бутон розы. Не забывайте через каждые 2 — 4 оборота смазывать клеем основание цветка. Получилось? Теперь остается сформировать очаровательный шар из цветов из гофрированной бумаги. Проделываете отверстия в пенопласте, клеевым пистолетом скрепляете форму, шпильку для волос, через которую легко пропускаете тесьму для подвешивания украшения. Налюбовавшись творением, приступаете к поиску новых идей: сочетания цветов, форм, добавление листочков, веточек, лент, бусинок, кусочков органзы придаст такой сказочный вид празднику, что захочется похвалить себя, талантливую и неподражаемую!
Paper Ball Run Challenge для классов 6-8
Планы уроков
Сумма
6-й-8-й
1-4 Студенты
2-3 часа
2-3 часа
Физика
Граждана Задача
Время, расстояние, скорость, силы, инженерный расчет
Бен Финио, доктор наук, друзья по науке
Эта инженерная задача основана на внутреннем конкурсе, разработанном сотрудниками корпорации Fluor.
Обзор
Добавьте изюминку в классическое занятие с помощью этого увлекательного плана урока. Ваши ученики спроектируют и построят дорожку для мяча для пинг-понга, используя только бумагу и скотч. Их цель состоит в том, чтобы сделать самых медленных мячей. Сколько времени они могут сделать, чтобы мяч прошел через их бег? Конкурс 2022 года завершен, но вы можете увидеть, что построили студенты, и узнать о победителях на итоговой странице 2022 Engineering Challenge. Учителя, обратите внимание, элементарный и средняя школа версии этого плана урока также доступны.
Адаптация к дистанционному обучению: Учащиеся могут посмотреть вводный видеоролик и следовать инструкциям в Рабочем листе для учащихся, чтобы построить и протестировать свои упражнения с мячом самостоятельно дома. Если вы хотите, чтобы учащиеся работали совместно, они могут делиться своими идеями друг с другом с помощью видеоконференций или общих документов/фотографий в Интернете.
Цели обучения
- Спроектировать бег с мячом на основе определенных критериев.
- Выберите дизайн, который будет работать лучше, на основе критериев.
- Создавайте и повторно тестируйте проекты.
Выравнивание NGSS
- MS-ETS1-2. Оцените конкурирующие проектные решения, используя систематический процесс, чтобы определить, насколько хорошо они соответствуют критериям и ограничениям проблемы.
Этот урок посвящен следующим аспектам трехмерного обучения NGSS:
| Научная и инженерная практика | Основные дисциплинарные идеи | Концепции поперечной резки | |||
| Научная и инженерная практика | Участие в споре с доказательствами. Оценивайте конкурирующие проектные решения на основе совместно разработанных и согласованных проектных критериев. Оценивайте конкурирующие проектные решения на основе совместно разработанных и согласованных проектных критериев. | Основные дисциплинарные идеи | ETS1.B: Разработка возможных решений.
Существуют систематические процессы для оценки решений относительно того, насколько хорошо они соответствуют критериям и ограничениям проблемы. | Концепции поперечной резки | Структура и функции. Конструкции могут быть спроектированы для выполнения определенных функций с учетом свойств различных материалов, а также того, как материалы могут быть сформированы и использованы. |
Материалы
Если вы хотите представить проекты своих учеников в конкурсе Engineering Challenge 2022, вы можете использовать только материалы, перечисленные ниже.
- Строительные материалы
- Бумага (максимум 30 листов).
 Допускаются бумага для принтера, чертежная, графическая и блокнотная бумага (формат Letter или A4; также разрешена плотная бумага размером 9 x 12 дюймов или 22 x 30 см). Карточки и газеты не допускаются .
Допускаются бумага для принтера, чертежная, графическая и блокнотная бумага (формат Letter или A4; также разрешена плотная бумага размером 9 x 12 дюймов или 22 x 30 см). Карточки и газеты не допускаются . - Лента (максимум один рулон), шириной не более 1 дюйма (2,5 см). Разрешены прозрачная офисная лента (например, Scotch®), малярная и малярная ленты. Двусторонняя лента, клейкая лента и упаковочная лента не разрешено .
- Плоская поверхность, например пол, стол или столешница
- Бумага (максимум 30 листов).
- Инструменты
- Ножницы
- Линейка
- Карандаш
- Рулетка или измерительная линейка
- Секундомер
- Мяч для пинг-понга, также известный как мяч для настольного тенниса (1)
Исходная информация для учителей
Этот раздел содержит краткий обзор для учителей естественных наук и понятий, затронутых в этом уроке.
Вы можете знать их под разными названиями: бег с мячом, бег по мрамору, машина с мячом или скульптура с катящимся мячом. Как бы вы их ни называли, эти устройства начинаются с по крайней мере одного шарика наверху, и этот шарик движется вниз по мере того, как он катится, отскакивает и проходит через различные объекты и препятствия (рис. 1).
Как бы вы их ни называли, эти устройства начинаются с по крайней мере одного шарика наверху, и этот шарик движется вниз по мере того, как он катится, отскакивает и проходит через различные объекты и препятствия (рис. 1).
Инженерное задание 2022 года вдохновлено бегом с мячом, как показано на рисунке 1. Как показано в видео, цель состоит в том, чтобы построить бег с мячом, используя только бумагу и ленту, но есть одна особенность. Ваши ученики хотят, чтобы мяч был равен долго как можно сделать это через мяч бежать. На рис. 2 показаны некоторые примеры типов бега с мячом, которые ваши учащиеся могут построить в этом проекте.
Этот проект можно использовать для изучения нескольких тем физики и техники со своими учениками. Вместо того, чтобы подробно объяснять каждую тему, в этом разделе «Основные сведения» вы найдете краткий обзор. Ссылки в разделе «Дополнительные сведения» содержат дополнительную информацию.
- Кинематика изучает движение. Как такие числа, как расстояние , время и скорость связаны? Какое отношение они имеют к траектории мяча и сколько времени требуется, чтобы пройти его?
- В беге с мячом используются различные формы энергии .
 Мяч имеет гравитационную потенциальную энергию , когда он находится в верхней части машины. Часть этой энергии преобразуется в кинетическую энергию (энергию движения) по мере того, как мяч набирает скорость. Часть этой энергии теряется на трение и преобразуется в тепловую энергию (тепло) при движении мяча. Когда мяч сталкивается или отскакивает от чего-либо, часть кинетической энергии преобразуется в другие формы, например акустическая энергия (звук).
Мяч имеет гравитационную потенциальную энергию , когда он находится в верхней части машины. Часть этой энергии преобразуется в кинетическую энергию (энергию движения) по мере того, как мяч набирает скорость. Часть этой энергии теряется на трение и преобразуется в тепловую энергию (тепло) при движении мяча. Когда мяч сталкивается или отскакивает от чего-либо, часть кинетической энергии преобразуется в другие формы, например акустическая энергия (звук). - В беге с мячом могут использоваться различные простые механизмы , такие как рычаги , наклонные плоскости (пандусы) или даже колесо и ось . Как ваши учащиеся могут включить различные простые механизмы в дизайн своих бега с мячом? Как они могут замедлить мяч?
- Если учащийся заставляет мяч бежать выше, мячу может понадобиться больше времени, чтобы пройти через него. Однако построить более высокую дорожку для мячей может быть сложно. Он должен быть прочным, чтобы не упасть.
 Например, учащимся может потребоваться соединить балки треугольной формы, чтобы сформировать фермы для поддержки высокого мяча.
Например, учащимся может потребоваться соединить балки треугольной формы, чтобы сформировать фермы для поддержки высокого мяча. - Вы можете использовать этот проект для отработки процесса инженерного проектирования со своими учениками. Им нужно будет спроектировать, построить и протестировать свои дорожки с мячом, а затем изменить их или внести улучшения и снова протестировать. Этот процесс называется итерация .
Подготовительные работы (15 минут)
Задействовать (5 минут)
Исследовать (1-2 часа)
Отражение (20 минут)
Оценить
Наладьте карьерные связи
Варианты плана урока
Изучите наши научные видеоролики
Изучите активность ферментов!
Угол наклона солнечной панели для Junior Solar Sprint
Двухступенчатая ракета на воздушном шаре. Введение
Введение
Создание сферы из плоского материала. Доктора-математики
(Новый вопрос недели)
шар из плоского материала призвал взглянуть на старый вопрос на ту же тему и некоторые новые идеи, в том числе мысли о приближении. И мы действительно видим физический результат нашей помощи, что бывает редко!Конструирование кожаной сферы
Вот вопрос от ноября прошлого года:
Может ли кто-нибудь научить меня, как определить окружности различных параллельных срезов или поперечных сечений сферы? Как если бы вы разрезали апельсин и сложили его заново — какова окружность в каждой точке, через которую прорезается нож. Я знаю, что в какой-то момент в школе я научился это делать, но это было много-много лет назад, и когда я пытаюсь посмотреть, все результаты касаются объема и площади поверхности, чего я не хочу.
Для контекста: я разрабатываю выкройки для пошива кожаных сумок разного размера. Я хочу, чтобы большая часть их тел имитировала сферическую форму, так как это приятно для глаз.
Для наброска моих первых шаблонов-прототипов было бы очень полезно иметь возможность начать с разметки математически определенных точек, чтобы у меня была хорошая (надеюсь, сферическая) основа для начала, и я мог бы затем создать шаблон, который производит как можно ближе к форма, которую я хочу получить в конечном продукте, без слишком большого количества переделок на швейной машине и меньшего количества отходов материала.
Спасибо за ваше время и любую помощь, которую вы можете оказать.
У Джессики есть хорошая идея сделать сферу из шести частей, а именно ширина каждой части на любом заданном уровне должна составлять 1/6 окружности сферы на этом уровне. Требуется немного больше работы (потому что высота, на которой каждая ширина будет находиться на изготавливаемой ею детали, должна быть измерена по окружности), но мы справимся. На самом деле, мы делали это уже 20 лет назад, поэтому я дал ссылку на тот, и на другой сайт, который я нашел:
Привет, Джессика.
То, что вы делаете, по сути, то, что делается для изготовления глобуса с использованием «клиньев» .
Ранее мы обсуждали это здесь, на сайте Ask Dr. Math :
Изготовление полусфер из бумаги
Я подумывал сделать об этом сообщение в блоге, включив в него изображения и конкретные примеры, чтобы точно прояснить, что делать. На самом деле, если вы дадите мне для примера конкретные цифры, мы сможем работать над этим вместе.
Между тем, вы можете выполнить поиск по термину «шаровидные борозды», чтобы найти дополнительную информацию и изображения. Сайтов с расчетами не нашел, но вот один дает конкретные указания по изготовлению глобуса (с более чем 6 гранями):
http://www.gma.org/surfing/imaging/globe.html
Беда в том, что ничего, что вы делаете с плоскими поверхностями, не может быть именно сферическим ; то, что вы предлагаете, всего с шестью клиньями, будет выглядеть явно шестиугольным сверху, , если материал не растягивается .
В результате может потребоваться сделать пару попыток, чтобы определить, какие размеры лучше всего подходят для вашего материала. Мы должны решить, должна ли ширина основываться на шестиугольнике, которым он будет на самом деле (хорды), или на сфере, которой вы хотите ее видеть (дуги). Вы можете сделать первую модель из бумаги или ткани, чтобы посмотреть, как она будет работать, но ваша первая модель из кожи может иметь другие свойства!
Итак, пришлите мне то, что вы хотите для первой попытки (радиус и высоту, если это не будет полная сфера), и я вернусь к вам с некоторыми цифрами и рисунком. Фактически, вы можете просто увеличить рисунок по мере необходимости, чтобы получить любой размер, при условии, что вы придерживаетесь шести клиньев.
Настоящие продукты обычно требуют (как и ожидала Джессика) первого математического наброска, модифицированного с учетом особенностей используемого материала. Мы увидим, что она такая же находчивая, как и другие мастера, которых я знал.
Изготовление бумажного полушария из клиньев
Прежде чем вернуться к этому разговору, давайте взглянем на страницу Спросите доктора Математики за 1999 год:
Изготовление полушарий из бумаги Я учитель математики в старшей школе, и я пытался понять, как бы вы сделали сферу из листа бумаги, например, если бы я хотел, чтобы мои ученики-геометрии взяли лист бумаги и сложили/разрезали его. так, чтобы он идеально вписался в северное полушарие земного шара. Сначала я решил, что сосредоточусь на том, как сложить лист бумаги в полусферу. Я думаю, что лучше всего было бы сделать Северный полюс центром фигуры. Я решил использовать треугольные клинья 30 градусов . Эти треугольные клинья на самом деле являются треугольниками, которые я изучал в неевклидовой геометрии , потому что их угловая мера превышает 180 градусов, где две конгруэнтные стороны, простирающиеся от Северного полюса до экватора, перпендикулярны экватору, но отстоят друг от друга на 30 градусов в с точки зрения продольных градусов.Я могу вычислить длину основания этого уникального равнобедренного треугольника, а также длины конгруэнтных катетов (поскольку я могу определить радиус). У меня есть проблема в том, как преобразовать эту цифру в лист бумаги. я знаю все три стороны этого треугольника изогнуты . Я также знаю, что все они являются частями больших кругов. Я не знаю, как на самом деле рисовать эти кривые или каков фактический угол для угла вершины этого равнобедренного треугольника. Какие кривые являются сторонами? Я знаю, что угол при вершине будет меньше 30 градусов при рисовании на плоском листе бумаги, но я не знаю, каким он будет в этом случае. Пожалуйста помоги! То, что я представлял для готового изделия (выкройка на плоском листе бумаги, которую можно разрезать/сложить так, чтобы получилась полусфера) этой фигуры было бы похоже на цветок, с северным полюсом в центре цветок, а каждый лепесток представляет один из неевклидовых треугольников. Пустые промежутки между этими «лепестками» были бы ненужной частью полушария, которую можно было бы загнуть или отрезать.
Спасибо за любую помощь, которую вы можете дать.
То, что Мэтт назвал «треугольниками», на самом деле представляет собой сферические треугольники с изогнутыми сторонами и изогнутой внутренней частью; ссылка на неевклидову геометрию уместна. Немного об этом см. в разделе Сумма углов треугольника в неевклидовой геометрии.
Вот изображение с сайта, на который я упомянул выше, показывающее набор из 12 клиньев, чтобы сделать глобус: большой *.
Доктор Рик ответил:
Привет, Мэтт. Я думаю, вы понимаете, что любая конструкция из вырезанной и/или сложенной бумаги не будет идеально накладываться на сферу . Чем уже вы сделаете свои клинья, тем ближе он подойдет, но идеальной сферы вы никогда не сделаете. Чтобы быть более конкретным, с 30-градусными клиньями любое поперечное сечение, параллельное экватору, будет иметь форму двенадцатиугольника, а не круга.
Экватор будет разделен на 12 равных частей по 30 градусов долготы каждая (как в примере выше).
Однако метод, который вы описываете, оказывается всего лишь тем, что делают производители глобусов . Они делают кусочки карты такой формы (которые они называют «клиньями») и приклеивают их на сферу.
Теперь давайте разработаем форму клиньев. Мы сделаем так, чтобы центральная линия каждого клинка лежала точно на сфере радиуса r. Назовите угловую ширину каждой борозды (количество градусов долготы, которую она покрывает) фи.
Посмотрите на произвольное поперечное сечение земного шара, параллельное экватору. Плоскость поперечного сечения встречается с поверхностью сферы на широте L. Я буду работать с коширотой (угол, измеренный от полюса) в радианах, которую я буду называть тета.
тета = (90 - L) * пи/180
Радиус окружности, являющейся поперечным сечением шара, равен
r_c = r*sin(тета)
Это можно увидеть, если взять другое поперечное сечение, перпендикулярное этому, содержащее ось сферы. Будет прямоугольный треугольник, гипотенуза которого равна r, один катет равен r_c, а противоположный угол равен тета.
Вот боковой разрез, о котором упоминал доктор Рик, и вид сверху, параллельный экватору (через линию широты):
E — точка на экваторе, N и S — полюса, а P — точка на окружности на широте L.
Поперечное сечение одного клинка представляет собой отрезок , касающийся окружности в ее центре. Мы хотим найти ширину W этого отрезка. Нарисуйте линию от центра круга до точки касания, а другую от центра до конца касательного сегмента (кровотока). Вы получаете прямоугольный треугольник с катетами длины r и W/2; угол, противоположный W/2, равен фи/2. Простая тригонометрия дает нам ширину крови как
W = 2*r_c*tan(фи/2)
= 2r*tan(фи/2)*sin(тета) Здесь я добавил к изображению одну клиновидную бороздку, показывающую, как рассчитывается ее ширина и как она загибается к полюсам:
Эти клинья предназначены для того, чтобы лежать вне сферы, так что с небольшими складками они могли прижиматься к сфере; если бы материал был растяжимым, вы могли бы сделать стороны, а не среднюю линию, каждой крови лежащей на сфере, и растянуть внутреннюю часть на сфере.
Расстояние (по дуге земного шара) от точки кровоизлияния до линии, ширину которой мы только что измерили, равно r*theta. (Помните, что тета измеряется в радианах.) Полная длина раны от кончика до кончика равна pi*r. (Кровь для полушария будет вдвое меньше, или pi*r/2.) Если вы разместите его на миллиметровой бумаге так, чтобы вершина находилась в начале координат, а центральная линия проходила вдоль оси X, то две стороны кровь будет лежать вдоль линий
y = +/- r*tan(phi/2)*sin(x/r)
Такова форма сторон «треугольника». Это синусоида, амплитуда которой определяется углом фи. В случае 6 клиньев \(\phi = \frac{2\pi}{6} = \frac{\pi}{3}\) или 60°. Тогда уравнение для каждой стороны клинка будет $$y = 0,57735r\sin\frac{x}{r}$$
Что касается угла у полюсов, то он _будет_ точно равен углу фи. Однако стороны начинают быстро изгибаться внутрь, поэтому мы говорим об угле между касательными к двум изогнутым линиям. Экваториальный конец «сферического треугольника» представляет собой вертикальную линию при x = pi*r/2, а синусоиды горизонтальны при x = pi*r/2, поэтому оба угла прямые.
Скоро у меня будет фотография крови.
Я не пробовал делать такие, поэтому не знаю, легко или сложно будет их собрать. Я бы попробовал использовать картон, а не тонкую бумагу, чтобы с ней было легче обращаться; Я вырезал клинья прямо по краям и приклеивал их вместе на внутренней стороне полусферы. Если бы это сработало, я бы подумал о более причудливых способах сделать это. Веселиться!
Это дает нам точную формулу формы запекшейся крови; но так как мы должны растянуть или сморщить кровь, чтобы сделать точную сферу, у нас есть, так сказать, некоторое «пространство для маневра». Джессика решила использовать его.
Достаточно хорошо для ручной работы
Ответ Джессики:
Привет, доктор Петерсон,
Спасибо, что ответили мне. Я не слишком беспокоюсь о том, чтобы форма была идеально точной , но я использую мягкую овчину толщиной всего 1-2 мм. Для своего теста я использовал валяный трикотаж, у меня были его обрезки, которые также хороши и толсты, чтобы проверить швы и тому подобное, по крайней мере, для той же толщины.
Но вы правы, кожа все равно будет вести себя немного по-другому.
Я пошел дальше и решил начать со второй ссылки, которую вы прислали. Я следовал указаниям вплоть до изготовления первой проточки, а затем провел на ней несколько измерений (умножил на 8 и разделил на 6), чтобы положить начало выкройке на миллиметровой бумаге. Получилось очень хорошо я думаю. Мне все еще нужно придумать, что я буду делать для закрытия верхней части, но это придет со временем. Начальный размер сферы, который я предположил, был с радиусом 2 дюйма.
Теперь, если бы я захотел сохранить эти точные измерения, которые я только что использовал, но в более крупном масштабе, я бы просто умножил каждое из них на одинаковую величину или это дало бы мне некоторые искажения?
Спасибо за всю помощь, я ценю это.
Три метода: вскрытие
Это было сделано не с помощью расчетов, разработанных доктором Риком, а с помощью метода, показанного на другой странице, на которую я дал ссылку. Ясно, что этого достаточно для целей Джессики; но для меня нам все еще нужно проверить метод и посмотреть, насколько он точен. Вот изображение построения с этой страницы, в котором используются круги, а не синусоиды формулы доктора Рика:
Ясно, что этого достаточно для целей Джессики; но для меня нам все еще нужно проверить метод и посмотреть, насколько он точен. Вот изображение построения с этой страницы, в котором используются круги, а не синусоиды формулы доктора Рика:
Вот мой собственный чертеж техники:
Прямоугольник ABCD имеет ширину, равную длине окружности (EF будет экватором), и высоту, равную половине окружности (точки на AD и BC будут на полюса). Разделим экватор на n равных частей и отметим G и H так, чтобы они совпали с серединой одной из них. Затем, просто предполагая, что кривая, которая нам нужна для запекшейся крови, представляет собой дугу окружности, мы находим центр K этой окружности с помощью стандартной конструкции (где перпендикуляр IJ к биссектрисе EG пересекает EF) и рисуем окружность. Затем мы повторяем это n раз. Обратите внимание, что в статье сказано использовать n = 8, а на чертеже n = 12; метод действителен для любых n (в той мере, в какой он действителен вообще).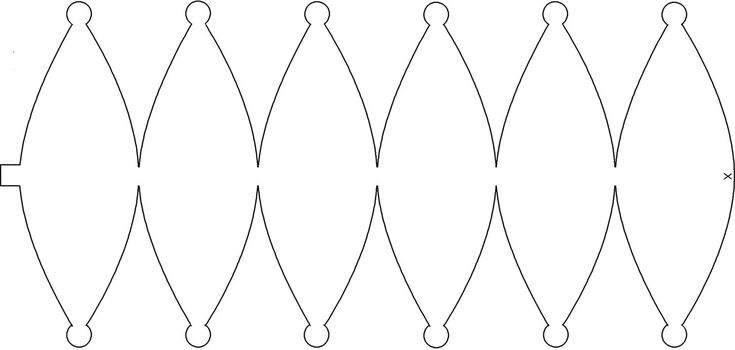
Я написал в ответ последние мысли об этом приближении:
Это выглядит великолепно и подтверждает мое мнение о том, что нам не нужна идеальная формула для получения хороших результатов.
Сайт, который вы использовали, дает грубое приближение, используя круг, к тому, что на самом деле является синусоидой . Вы можете сделать ту же конструкцию для другого количества клиньев, просто разделив большой прямоугольник на 6, а не на 8 частей, и проделав после этого ту же работу.
Похоже, что Джессика только что увеличила горизонтальные размеры модели с 8 лезвиями на 8/6, и результат был достаточно хорош; общий случай построения (принимая n = 6, а не 8) был бы немного другим, но на самом деле не лучше.
Я также попробовал несколько иной метод, чем метод доктора Рика, сделав ширину не шириной касательной, а шириной дуги самой сферы, для сравнения (исходя из теории, что растяжение может дать лучшие результаты, и поскольку это была собственная методика Джессики). предложение):
предложение):
Выполняя собственные расчеты и делая ширину кровавой раны (согласно вашему вопросу) частью окружности сферы, я получаю уравнение кривой с каждой стороны от нее как
y = R (pi/N) cos(x/R)
, где x — расстояние от центра, R — радиус сферы, а N — количество клиньев. Для сравнения, формула доктора Рика дает ширину запекшейся крови в виде касательной (как если бы вы разрезали ее по жесткой бумаге; его формула, переведенная на мой язык, равна 9).0003
y = R tan(pi/N) cos(x/R)
Итак, теперь у нас есть три формулы для формы крови: синусоида доктора Рика, моя, которая немного уже, но все же синусоида, и дуга окружности другого источника.
Я нарисовал обе эти кривые и кружок для N=6 (у меня красный, у Рика синий, кружок пунктирный) ниже. Вы можете видеть, что они относительно близки. Если вас не устраивает то, что вы уже сделали, вы можете попробовать использовать одну из других кривых.
(я также нарисовал растянутую версию Джессики с 8 лезвиями, и здесь она практически неотличима от пунктирной кривой.


 Допускаются бумага для принтера, чертежная, графическая и блокнотная бумага (формат Letter или A4; также разрешена плотная бумага размером 9 x 12 дюймов или 22 x 30 см). Карточки и газеты не допускаются .
Допускаются бумага для принтера, чертежная, графическая и блокнотная бумага (формат Letter или A4; также разрешена плотная бумага размером 9 x 12 дюймов или 22 x 30 см). Карточки и газеты не допускаются .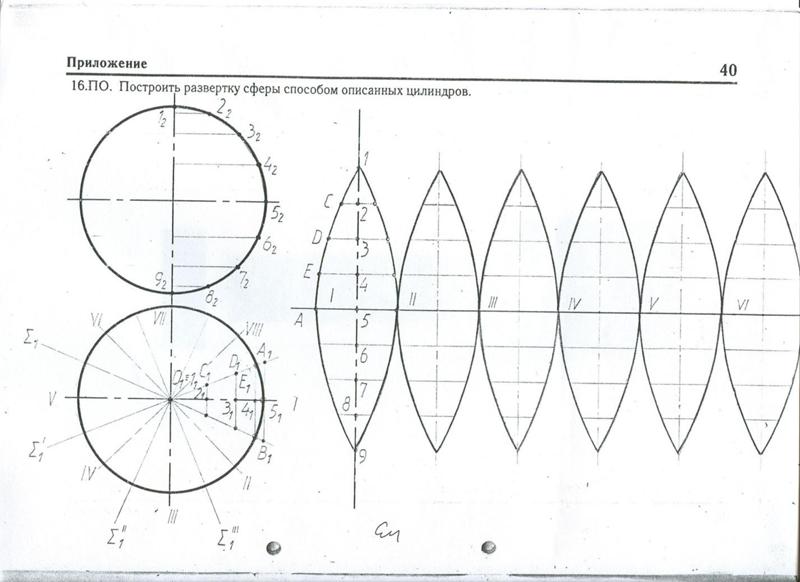 Мяч имеет гравитационную потенциальную энергию , когда он находится в верхней части машины. Часть этой энергии преобразуется в кинетическую энергию (энергию движения) по мере того, как мяч набирает скорость. Часть этой энергии теряется на трение и преобразуется в тепловую энергию (тепло) при движении мяча. Когда мяч сталкивается или отскакивает от чего-либо, часть кинетической энергии преобразуется в другие формы, например акустическая энергия (звук).
Мяч имеет гравитационную потенциальную энергию , когда он находится в верхней части машины. Часть этой энергии преобразуется в кинетическую энергию (энергию движения) по мере того, как мяч набирает скорость. Часть этой энергии теряется на трение и преобразуется в тепловую энергию (тепло) при движении мяча. Когда мяч сталкивается или отскакивает от чего-либо, часть кинетической энергии преобразуется в другие формы, например акустическая энергия (звук). Например, учащимся может потребоваться соединить балки треугольной формы, чтобы сформировать фермы для поддержки высокого мяча.
Например, учащимся может потребоваться соединить балки треугольной формы, чтобы сформировать фермы для поддержки высокого мяча. Для наброска моих первых шаблонов-прототипов было бы очень полезно иметь возможность начать с разметки математически определенных точек, чтобы у меня была хорошая (надеюсь, сферическая) основа для начала, и я мог бы затем создать шаблон, который производит как можно ближе к форма, которую я хочу получить в конечном продукте, без слишком большого количества переделок на швейной машине и меньшего количества отходов материала.
Для наброска моих первых шаблонов-прототипов было бы очень полезно иметь возможность начать с разметки математически определенных точек, чтобы у меня была хорошая (надеюсь, сферическая) основа для начала, и я мог бы затем создать шаблон, который производит как можно ближе к форма, которую я хочу получить в конечном продукте, без слишком большого количества переделок на швейной машине и меньшего количества отходов материала.
 В результате может потребоваться сделать пару попыток, чтобы определить, какие размеры лучше всего подходят для вашего материала. Мы должны решить, должна ли ширина основываться на шестиугольнике, которым он будет на самом деле (хорды), или на сфере, которой вы хотите ее видеть (дуги). Вы можете сделать первую модель из бумаги или ткани, чтобы посмотреть, как она будет работать, но ваша первая модель из кожи может иметь другие свойства!
В результате может потребоваться сделать пару попыток, чтобы определить, какие размеры лучше всего подходят для вашего материала. Мы должны решить, должна ли ширина основываться на шестиугольнике, которым он будет на самом деле (хорды), или на сфере, которой вы хотите ее видеть (дуги). Вы можете сделать первую модель из бумаги или ткани, чтобы посмотреть, как она будет работать, но ваша первая модель из кожи может иметь другие свойства! Я могу вычислить длину основания этого уникального равнобедренного треугольника, а также длины конгруэнтных катетов (поскольку я могу определить радиус). У меня есть проблема в том, как преобразовать эту цифру в лист бумаги. я знаю все три стороны этого треугольника изогнуты . Я также знаю, что все они являются частями больших кругов. Я не знаю, как на самом деле рисовать эти кривые или каков фактический угол для угла вершины этого равнобедренного треугольника. Какие кривые являются сторонами? Я знаю, что угол при вершине будет меньше 30 градусов при рисовании на плоском листе бумаги, но я не знаю, каким он будет в этом случае. Пожалуйста помоги!
То, что я представлял для готового изделия (выкройка на плоском листе бумаги, которую можно разрезать/сложить так, чтобы получилась полусфера) этой фигуры было бы похоже на цветок, с северным полюсом в центре цветок, а каждый лепесток представляет один из неевклидовых треугольников. Пустые промежутки между этими «лепестками» были бы ненужной частью полушария, которую можно было бы загнуть или отрезать.
Я могу вычислить длину основания этого уникального равнобедренного треугольника, а также длины конгруэнтных катетов (поскольку я могу определить радиус). У меня есть проблема в том, как преобразовать эту цифру в лист бумаги. я знаю все три стороны этого треугольника изогнуты . Я также знаю, что все они являются частями больших кругов. Я не знаю, как на самом деле рисовать эти кривые или каков фактический угол для угла вершины этого равнобедренного треугольника. Какие кривые являются сторонами? Я знаю, что угол при вершине будет меньше 30 градусов при рисовании на плоском листе бумаги, но я не знаю, каким он будет в этом случае. Пожалуйста помоги!
То, что я представлял для готового изделия (выкройка на плоском листе бумаги, которую можно разрезать/сложить так, чтобы получилась полусфера) этой фигуры было бы похоже на цветок, с северным полюсом в центре цветок, а каждый лепесток представляет один из неевклидовых треугольников. Пустые промежутки между этими «лепестками» были бы ненужной частью полушария, которую можно было бы загнуть или отрезать.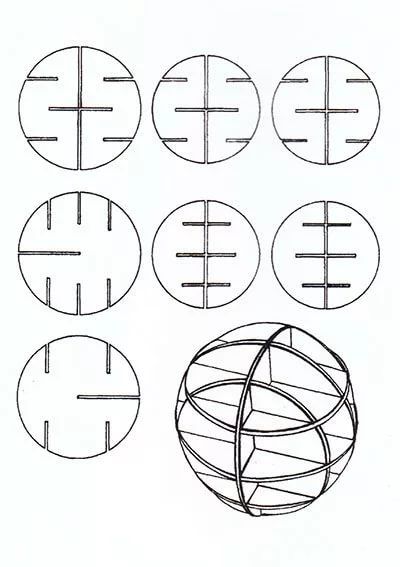 Спасибо за любую помощь, которую вы можете дать.
Спасибо за любую помощь, которую вы можете дать. 

 Но вы правы, кожа все равно будет вести себя немного по-другому.
Но вы правы, кожа все равно будет вести себя немного по-другому.